Draw Circle Between Two Points Om Google Map

Wherein our heroes find that the shortest distance between two points on a globe is not a straight line, afterward all.

What's so great about a great circle? A neat circle, technically speaking, is any circle that goes all the mode around a sphere, with its center on the exact center point of the sphere. Equally it turns out, when a great circle connects two points on a sphere, the arc betwixt them is always the shortest distance between those two points. Naturally, being able to take the shortest possible path is a matter of peachy financial and practical importance in this modern era of air travel.

Familiar 2-dimensional map projections don't give a adept impression of swell-circumvolve distance. On a Mercator map, the straight line that seems to exist the shortest route between San Francisco and London passes through Boston; but, in fact, due to the curvature of the globe, the actual shortest route runs nearer to the North Pole, passing over the south of Greenland.

This hack makes use of Generic Mapping Tools, or GMT [Hack #28] to show how to plot segments of a great circle on many different cartographic projections, including those designed for marine and aeriform navigation. Nosotros'll also bear witness you how you can attempt this yourself with a quick Perl script.

iii.10.1. Great Circles on a Mercator Projection

The Mercator projection was historically useful because it preserved navigational direction forth lines of abiding bearing, known as rhumb lines. One could draw a directly line to one's destination on the map, set off in the direction indicated by that line, and actually get in at the intended destination one-time in the time to come. Navigating by a Mercator map therefore had the groovy reward of simplicity, but the disadvantage was that the rhumb line between two points was often not the shortest path.

Instead, the shortest path between ii points follows a line of variable bearing, which turns out to exist the arc of a cracking circle. This may seem counterintuitive, because a great-circle arc will commonly end upward looking curved on a flat map. Figure 3-31 depicts the bang-up-circle arc connecting San Francisco and London on a Mercator project of the world.

Figure 3-31. Groovy-circle arc from SF to London on a Mercator project

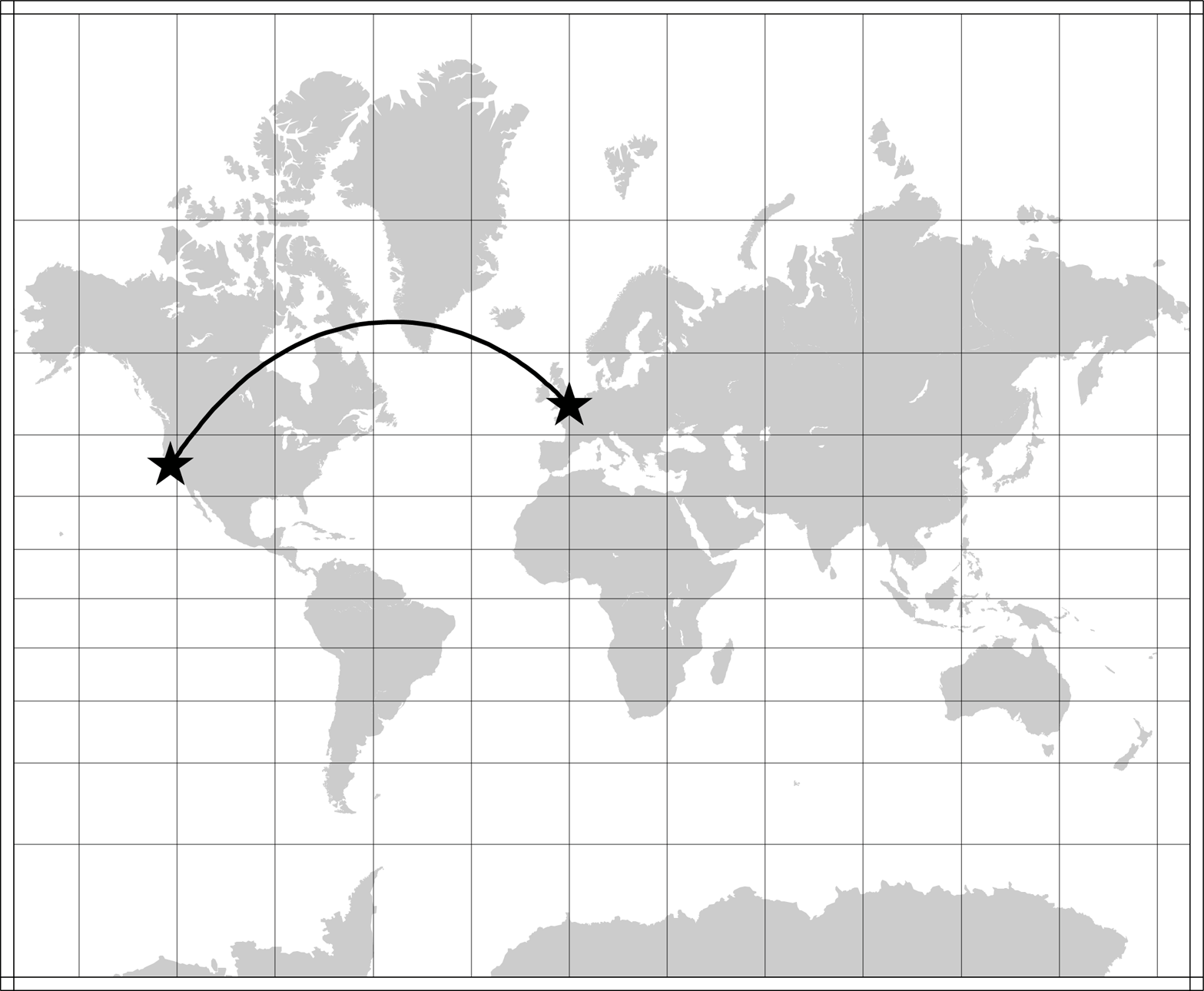
The post-obit commands, using pscoast and psxy from GMT, were used to generate Figure 3-31:

$          pscoast -JM18c -R-170/190/-75/85 -Bg30/g15 -A5000 -G192/192/192 -K >   mercator.ps          $          psxy points.txt -JM18c -R-170/190/-75/85 -W8 -O -K >> mercator.ps          $          psxy points.txt -JM18c -R-170/190/-75/85 -Sa.75c -G0/0/0 -O >> mercator.ps        

The call to pscoast draws the graticule (i.e., grid lines) and the base map of the continents. Nosotros recommend reviewing [Hack #28] to sympathize exactly how these particular pscoast options do their magic. The first call to psxy really draws the neat-circle arc into the aforementioned file. We give psxy the aforementioned projection parameters we did pscoast, along with a filename, points.txt. The points.txt file simply contains the following:

-122,38 0,51

The geographically savvy reader volition recognize these as the longitude and latitude coordinates of San Francisco and London, respectively. The -W8 pick to psxy tells information technology to make the great-circle arc eight pixels thick. Finally, we telephone call psxy one more time, with the same projection parameters and filename containing our points, but this fourth dimension we give the -Southward option to asking that symbols be fatigued at each point, instead of a line connecting them. In this case, the -Sa.75c option draws us a star .75 centimeters wide at each end bespeak, coloring each one black via the -G option.

The shortest line between two points on any geometric figure is referred to as a geodesic, of which the great circle along a spherical surface is merely an instance. For this reason, the GRASS command for cartoon great circles is called r.geodesic. The word geodesic, which comes from the Greek words for "dividing the Earth," is besides used to depict Buckminster Fuller's dome structures, in the way that they systematically divide the surface of a sphere (or hemisphere) into triangular faces.

three.x.2. Smashing Circles on an Orthographic Projection

The fact that a slap-up circle forms the shortest line between two points doesn't seem quite as odd, yet, when yous await at a globe. Figure three-32 depicts the same smashing-circle arc connecting San Francisco and London on an orthographic projection, which presents a flat perspective view of a globe. From this vantage, it becomes evident that the shortest route from San Francisco to London actually does sort of run over the curve of the earth, as it were, rather than around it. Consequently, the line that runs between them through Bostonthe line one might have thought was the shortest, looking at a Mercator mapis really quite hopelessly roundabout.

Figure 3-32. Bully-circumvolve arc from San Francisco to London on an orthographic projection

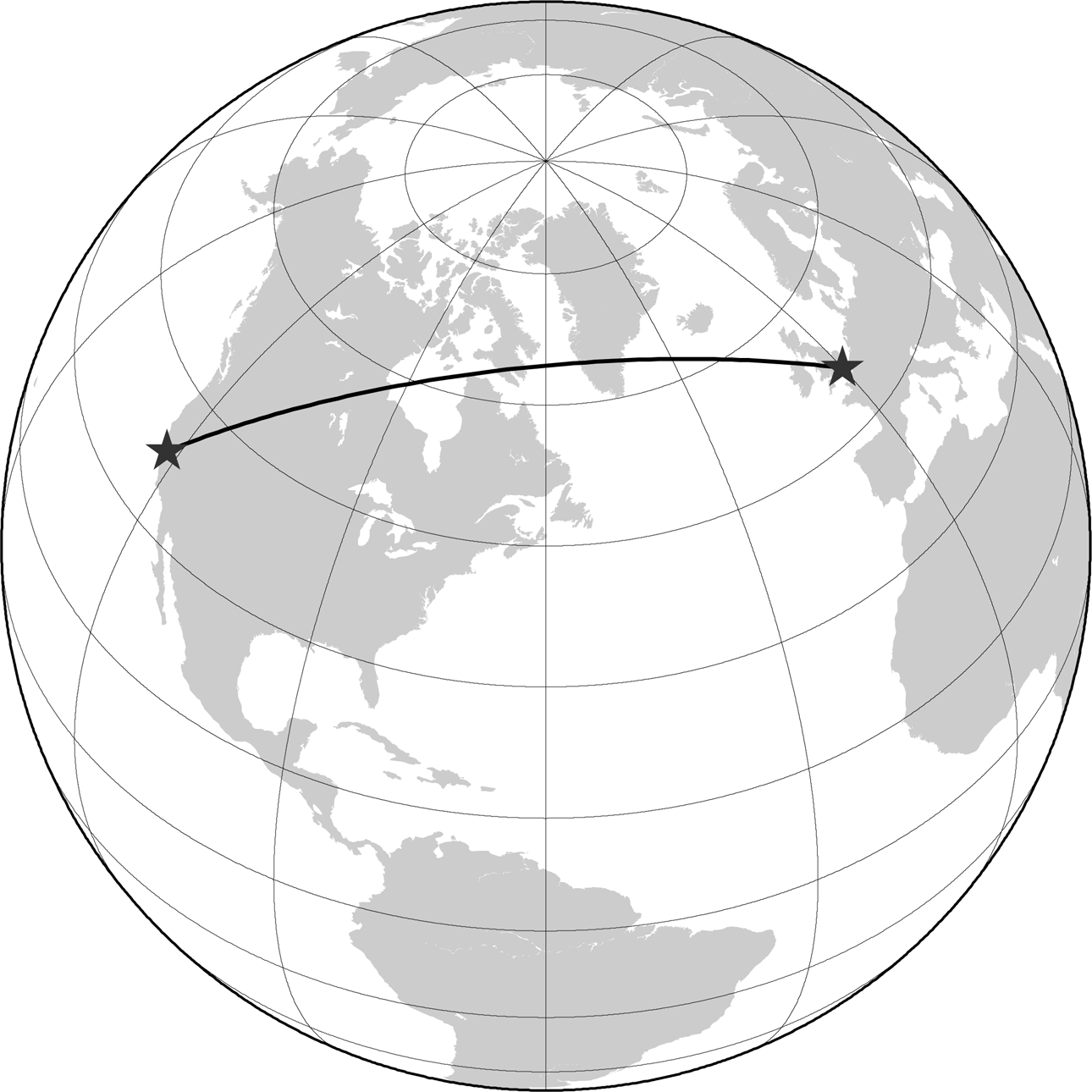
Figure 3-32 was made using the aforementioned GMT commands equally Figure iii-31, except that the -JM18c parameter for generating a Mercator projection was replaced with -JG-lx/45/18c, which draws an orthographic projection xviii centimeters wide, centered on 60º W and 45º N.

3.10.iii. Great Circles on a Gnomonic Projection

There are other ways to visualize keen circles on a apartment map, of grade. If we want a map that depicts the shortest distance between 2 points as a straight line, we tin plough to the Gnomonic project. Basically, whatsoever directly line on a Gnomonic projection, regardless of origin or begetting, represents a great-circumvolve arc on Earth'due south surface. Although the Gnomonic projection distorts the shape and area of landmasses something fierce, the property of showing any great-circle arc every bit a straight line makes information technology quite useful for the purposes of air navigation. Effigy 3-33 shows the great circle connecting London and San Francisco on a Gnomonic projection of the earth. Figure 3-33 was generated with GMT in the same way equally Figures 3-31 and iii-32, using the -JF-75/60/threescore/18c choice to plot the Gnomonic projection centered on 75º W and 60º North, with a radius of 60º.

Figure 3-33. Not bad-circle arc from San Francisco to London on a Gnomonic projection

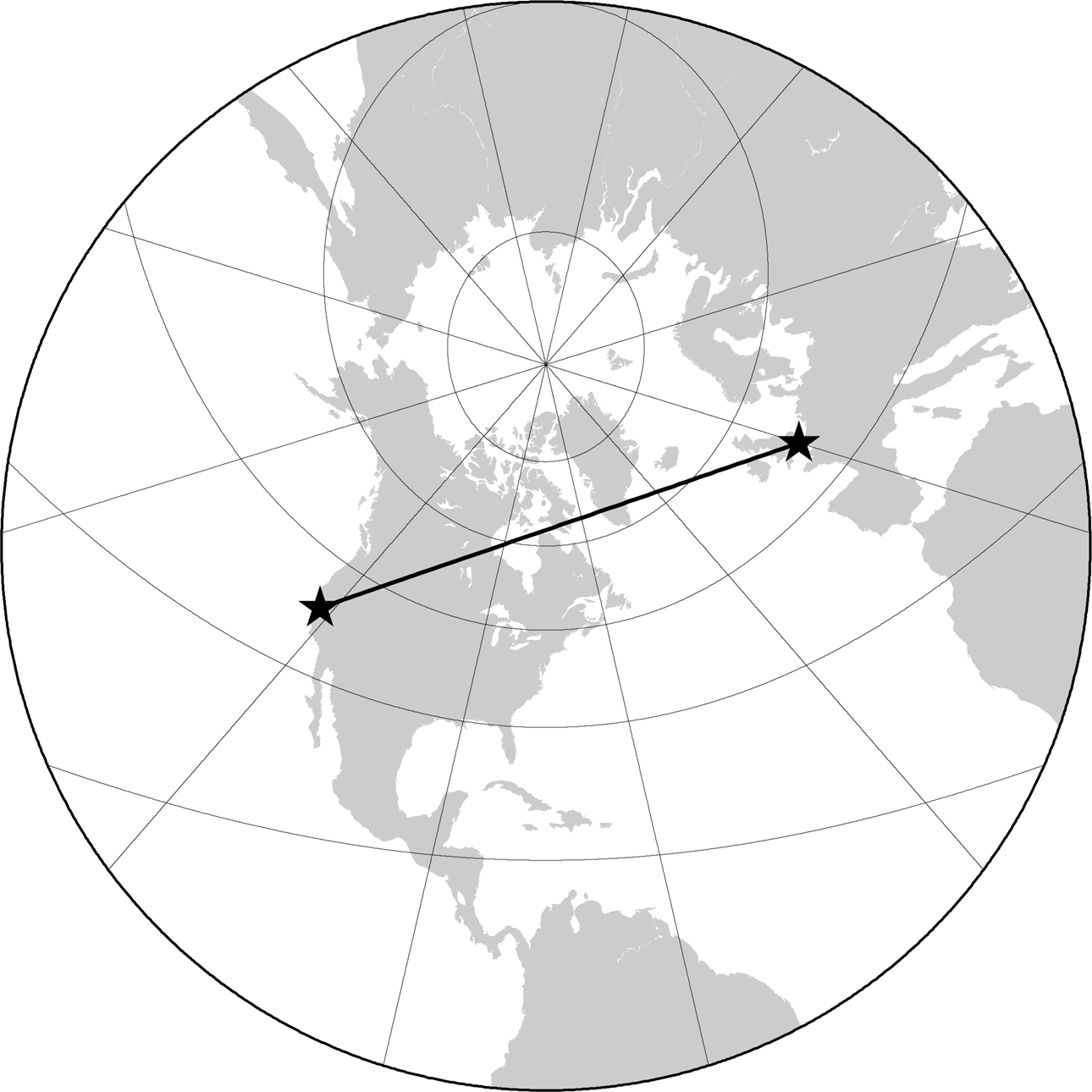
3.10.4. Nifty Circles of Perl

In practice, keen-circle routes are difficult to navigate precisely, because the bearing of a not bad circle relative to True North changes continually, unlike that of a rhumb line. In fact, the conventional fashion to navigate a great-circle route is to approximate information technology with a serial of curt rhumb lines. Nosotros tin can employ this same technique to draw the path of a groovy-circumvolve arc on a apartment map in Perl:

#!/usr/bin/perl   apply Math::Trig qw(great_circle_direction deg2rad); apply Imager; use strict;   my ($mapfile, $lon1, $lat1, $lon2, $lat2) = @ARGV; my @origin = ($lon1, $lat1); my @dest = ($lon2, $lat2); my $stride = .1;   my @position = @origin; my @points;   until (abs($position[0] - $dest[0]) < $footstep  and abs($position[1] - $dest[1]) < $stride) {  my $bearing = great_circle_direction(  deg2rad( $position[0] ),  deg2rad( ninety - $position[1] ),  deg2rad( $dest[0] ),  deg2rad( 90 - $dest[1] )  );    $position[0] += sin($bearing) * $pace / cos(deg2rad($position[one])) ;  $position[1] += cos($begetting) * $step;    $position[0] += 360 if $position[0] < -180;  $position[0] -= 360 if $position[0] > 180;    push button @points, @position; }

In the commencement part of our script, we do the actual approximation of rhumb lines to a swell circle, using the great_circle_direction() part from the Math::Trig module, which ships with Perl. We go the name of an image containing an Equidistant Cylindrical project, as well as the longitude and latitude of our start and finish points from the command line. We set @origin to the longitude and latitude of our starting betoken, and @dest to that of our destination. $step is called to roughly estimate the length of each component rhumb line. The current position is stored in @position, which gets initialized to our origin.

At each step, we call great_circle_direction() to find the begetting from True North at our current position forth the great circle to our destination. Since great_circle_direction() expects its arguments in radians, non degrees, and places the zero latitude at the North Pole, rather than the equator, we have to brand the proper adjustments before passing those values. Nosotros store the result in radians in $begetting, which we and then use to update our current position.

Updating the latitude of our current position, as stored in $position[1], is easy: simply add the cosine of our begetting scaled past the length of our rhumb line to find the latitude of our side by side terminate point. If you dig deep into the mists of your high school trigonometry education, you'll remember why this is then: If we take $pace to exist the length of the hypotenuse of a right triangle, then the cosine of the begetting is equal to the length of the adjacent side divided by the length of the hypotenuse.

Multiplying both sides of the equation by $step yields the code shown before for updating $position[i].

Updating the longitude, all the same is a niggling trickier. Nosotros could simply take our electric current longitude, stored in $position[0], and add together the sine of our electric current bearing, scaled by the length of our rhumb line, but we would exist ignoring an important fact about our round world. As you head toward the poles, the altitude between two lines of longitude gets shorter in proportion to the cosine of the latitude. At the equator, the distance separating one degree of longitude is cos(0º) = 1 degree of breadth. At the Due north Pole, the distance is cos(90º), which is cipher. Thus we divide our longitude increase by the cosine of the current breadth, in order to continue in step with the actual great- circle arc.

Actually, we fibbed slightly. The distance separating 1 degree of longitude at the equator isn't quite equal to 1 degree of latitude, because Globe isn't a perfect sphere it's an oblate spheroid, which means it'south slightly flattened at the poles and slightly bulged around the middle, due to rotational and tidal forces. Because the difference is insignificant for our purposes, though, we'll otherwise ignore this fact in our discussion.

Finally, we practice some premises checking, to keep our longitude from running off the edge of the map. Having done and then, we add our new electric current position to @points, and repeat, until we're shut enough to our destination that information technology'south not worth continuing.

Now that we have a list of longitude/latitude coordinates in @points, representing the stop points of the rhumb line segments that approximate our great-circle arc, we can employ any suitable method to plot them on a flat map. For simplicity's sake, we'll use the method outlined in [Hack #29] to draw the nifty-circle arc between San Francisco and London on an Equidistant Cylindrical map of the world. The remainder of our script, and then, reads as follows:

my ($top, $left) = ( 90, -180 ); my ($bottom, $correct) = ( -90, 180 );   my $map = Imager->new; $map->open( file => $mapfile ) or die $map->errstr;   my $x_scale = $map->getwidth / ($right - $left); my $y_scale = $map->getheight / ($bottom - $top);   while (@points) {  my (@ten, @y);  while (my ($lon, $lat) = splice @points, 0, 2) {  push @x, ($lon - $left) * $x_scale;  push @y, ($lat - $top) * $y_scale;  last if @points and $lon < -170 and $points[0] > -170;  }  $map->polyline( x => @x, y => @y, color => "crimson" ); }   $map->write( fh => *STDOUT, blazon => "jpeg" ) or die $map-> errstr;

Since this method of plotting points on a rectangular map [Hack #29] is explained elsewhere, we'll gloss over the details here. We load the map image stored before in $mapfile into an object stored in $map. The crucial bit happens in the while() loop, where we shift coordinate pairs off of @points, and convert the longitude and latitude to x- and y-coordinates on the map image. One time we've done this, we send our lists of 10 and y end points to $map->polyline(), to draw the actual arc on the map. Nosotros have to exist sure to test for the example where the arc crosses the international date line, and break the polyline into two parts, if necessary. The last if @points... argument tests for this possibility. Finally, the map is dumped to standard output. The code to run is every bit follows:

$          perl greatcircle.pl PathfinderMap.jpg -122 38 0 51 > sf_to_london.jpg        

Nosotros give the script the name of our Equidistant Cylindrical map file [Hack #29] for good sources of such maps), also as the longitude and latitude of San Francisco and London, in that society. The map, which is shown in Figure iii-34, shows the groovy-circumvolve arc connecting them. Adding embellishments, such as a mark at each finish, is left equally an exercise for the reader.

Effigy 3-34. Great-circle arc from SF to London, plotted with Perl, on a Equidistant Cylindrical project

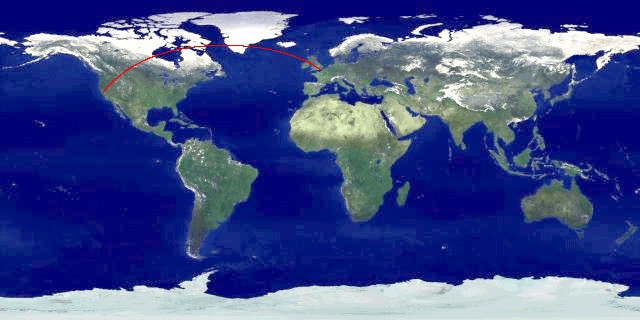
Of grade, having found the shortest route from San Francisco to London, you will probably immediately want to know how long that route is, which is a question tackled in [Hack #27] .

3.10.5. Run across Also

• [Hack #28]
• [Hack #29]
• [Hack #27]

andujarthwary.blogspot.com

Source: https://flylib.com/books/en/2.366.1/hack_30_plot_a_great_circle_on_a_flat_map.html

Share this post